Probabilidad Binomial

La probabilidad binomial es una medida de la probabilidad de obtener con éxito una cierta cantidad de ocurrencias de un número total de ensayos. Por ejemplo, imagine que ha plantado guisantes que produjeron varios crías. También imagine que, a partir de pruebas anteriores, se han dado cuenta de que la probabilidad de obtener guisantes verdes de su granja es de 0,75. Ahora imagine que usted planta algunos guisantes y producen cinco descendientes. Es posible que desee averiguar la probabilidad de obtener tres guisantes.

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace ProbabilidadBinomial_I
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private static long Factorial(long x)
        {
            if (x <= 1)
                return 1;
            else
                return x * Factorial(x - 1);
        }

        private static long Combination(long a, long b)
        {
            if (a <= 1)
                return 1;

            return Factorial(a) / (Factorial(b) * Factorial(a - b));
        }

       private double ProbabilidadBinomial (int ensayos, int aciertos, double probabilidad)
        {
            double fallos = 1 - probabilidad;
            double c = Combination(ensayos, aciertos);
            double px = Math.Pow(probabilidad, aciertos);
            double qnx = Math.Pow(fallos, ensayos - aciertos);
            return c * px * qnx;
        }

Factor Primo

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

namespace FactoresPrimosNumero_Forms

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        private void button2_Click(object sender, EventArgs e)

        {

            Application.Exit();

        }

        private void button1_Click(object sender, EventArgs e)

        {

            int numero, resi, k;

            string cadena = textBox2.Text;

            numero = int.Parse(textBox1.Text);

            k = 2;

            if (!int.TryParse(textBox1.Text, out numero)) numero = -1;

            if (numero < 2)

            {

                MessageBox.Show("Numeros negativos NO. \r\n Superiores a 2 por favor");

                textBox1.Clear();

                return;

            }

            while ((numero != 1))

            {

                resi = numero % k;

                if ((resi == 0))

                {

                    cadena += (k.ToString() + " x ");

                    textBox2.Text = cadena.Remove(cadena.Length - 2);

                    numero = numero / k;

                }

                else

                {

                    k = k + 1;

                }

            }

        }

Entropía de Shannon

"El hombre más importante del que probablemente no hayas oído hablar jamás."

En el ámbito de la teoría de la información la entropía, también llamada entropía de la información y entropía de Shannon (en honor a Claude E. Shannon), mide la incertidumbre de una fuente de información.

La entropía también se puede considerar como la cantidad de información promedio que contienen los símbolos usados. Los símbolos con menor probabilidad son los que aportan mayor información; por ejemplo, si se considera como sistema de símbolos a las palabras en un texto, palabras frecuentes como «que», «el», «a» aportan poca información, mientras que palabras menos frecuentes como «corren», «niño», «perro» aportan más información. Si de un texto dado borramos un «que», seguramente no afectará a la comprensión y se sobreentenderá, no siendo así si borramos la palabra «niño» del mismo texto original. Cuando todos los símbolos son igualmente probables (distribución de probabilidad plana), todos aportan información relevante y la entropía es máxima.

El concepto entropía es usado en termodinámica, mecánica estadística y teoría de la información. En todos los casos la entropía se concibe como una «medida del desorden» o la «peculiaridad de ciertas combinaciones». La entropía puede ser considerada como una medida de la incertidumbre y de la información necesarias para, en cualquier proceso, poder acotar, reducir o eliminar la incertidumbre. Resulta que el concepto de información y el de entropía están básicamente relacionados entre sí, aunque se necesitaron años de desarrollo de la mecánica estadística y de la teoría de la información antes de que esto fuera percibido.

Claude Elwood Shannon (30 de abril de 1916 – 24 de febrero de 2001) fue un matemático, ingeniero eléctrico y criptógrafo estadounidense recordado como «el padre de la teoría de la información».

Shannon es reconocido por haber fundado el campo de la teoría de la información con la publicación Una teoría matemática de la comunicación, que supuso un hito en 1948. Es quizás igualmente conocido por haber sentado las bases de la teoría del diseño del ordenador digital y el circuito digital en 1937. Con 21 años, mientras realizaba su maestría en el Massachusetts Institute of Technology (MIT), demostró con su tesis, que las aplicaciones electrónicas de álgebra booleana podrían construir cualquier relación lógico-numérica. Shannon contribuyó asimismo al campo del criptoanálisis para la defensa de Estados Unidos durante la Segunda Guerra Mundial, con trabajos sobre el descifrado de códigos y la seguridad en las telecomunicaciones.
Claude Elwod Shannon definió una forma de medir la cantidad de información que contiene una variable aleatoria, es lo que se conoce como Entropía de Shannon y su formula es la siguiente:

Esta obra está bajo una: Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional. Autor: Ondiz Zarraga
 https://ondahostil.wordpress.com/2015/04/16/lo-que-he-aprendido-entropia-de-shannon/

                       The Man Who Turned Paper Into Pixels from Adam Westbrook on Vimeo.

La entropía definida por Shannon , referida a la teoría de la información, hace referencia a la cantidad media de información que contiene una variable aleatoria (psicológica) o, en particular, una fuente transmisión binaria. La información que aporta un determinado valor, xi, de una variable aleatoria discreta X, se define como:

I(xi) = log2(1/p(xi))

cuya unidad es el bit si se utiliza el logaritmo en base 2 (por ejemplo, cuando se emplea el logaritmo neperiano o natural se habla de nats).

La entropía o información media de la variable aleatoria discreta, X, se determina como la información media del conjunto de valores discretos que puede adoptar (también medida en bits):

H(x) = Σip(xi) •log2(1/p(xi))


using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace EntropíaShannon_I
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        public static double logaritmo(double num)
        {
            return Math.Log(num) / Math.Log(2);
        }
        private void button2_Click(object sender, EventArgs e)
        {

            string entrada = textBox1.Text;
            double entropia = 0;
            Dictionary<char, double> tabla = new Dictionary<char, double>();

Números Catalán del Triangulo de Pascal

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace CatalanNumberTrianguloPascal_I
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        int limite;

        private void button1_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            int n = limite;

            limite = int.Parse(textBox1.Text);

            List<int> t = new List<int>() { 0, 1 };

            for (int i = 1; i <= n; i++)
            {
                for (var j = i; j > 1; j--) t[j] += t[j - 1];

                t.Add(t[i]);

                for (var j = i + 1; j > 1; j--) t[j] += t[j - 1];
                {
                    listBox1.Items.Add((((i == 1) ? "                  " : "                  ") + (t[i + 1] - t[i])) + "\r\n");
                }

            }

        }
    }
}

Número de Munchausen

Un número de Munchausen (o Münchhausen) es un número natural n el cual la suma de sus dígitos (en base 10), elevados a la misma potencia de ellos mismos es el mismo número es decir n. En otras palabras, si el número tiene la representación decimal:

Entonces:

El término fue acuñado por el ingeniero de software y matemático holandés Daan van Berkel en 2009. El nombre se debe a que cada dígito está "elevado" por si mismo, esto evoca la historia de Barón Munchausen que se elevo a si mismo hacia arriba jalando su propia coleta. Los números narcisistas siguen una regla similar, pero en el caso de los números narcisistas la potencia de los dígitos es fija, siendo elevados a la potencia del número de dígitos en el número. Esto es una explicación adicional para el nombre, dado que el Barón Münchhausen era un conocido narcisista.

Pensando rápido, posiblemente encontréis el primer número Münchhausen, el 1. Pero si seguís probando, estaréis mucho tiempo hasta encontrar el siguiente número Münchhausen. De hecho, si no os valéis de un ordenador, posiblemente pasarían días y mucho aburrimiento hasta que llegaseis al número 3435 (siempre hablando en base 10).
Estos números en muchas ocasiones se considera un grupo dentro de los números narcisistas, agrupándolos con los números de Armstrong (los que normalmente son llamados narcisistas), los números de Dudeney o los números de Friedman.

Un ejemplo es:

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

namespace MunchausenForms_I

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        int limite;

        private void button1_Click(object sender, EventArgs e)

        {

            Application.Exit();

        }

Números Lychrel

Un número de Lychrel es un número natural que no puede formar un palíndromo a través del proceso iterativo repetitivo de invertir sus dígitos y sumar los números resultantes. Este proceso es a veces llamado algoritmo-196 (en inglés 196-algorithm), a raíz del número más famoso asociado con el proceso. En base decimal, no ha sido demostrado que los números de Lychrel existan, pero algunos, incluyendo el 196, son sospechosos por motivos estadísticos y de heurística. El nombre «Lychrel» fue acuñado por Wade VanLandingham como un anagrama aproximado de Cheryl, el nombre de su novia.

A partir de un número inicial en base decimal, se realiza la suma de este y su número invertido, es decir, el número resultante de la inversión del orden en el que aparecen sus dígitos. Por ejemplo, para 124 se tiene que 124 + 421 = 545. Repitiendo el mismo proceso con los números resultantes, si alguno de ellos es un palíndromo, entonces el número inicial no es un número de Lychrel.

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using IntXLib;


namespace Lychrel_IV_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        int numeromaximo;

        private void button1_Click_1(object sender, EventArgs e)
        {
            numeromaximo = int.Parse(textBox1.Text);
            int contador = 0;
            for (int i = 1; i < numeromaximo; i++)
            {
                IntX iteracionTotal = new IntX(i);

                for (int iteracion = 0; iteracion < 51; iteracion++)
                {
                    if (iteracion == 50)
                    {
                        listBox1.Items.Add(i.ToString() + " Lychrel");
                        contador++;
                        break;
                    }
                    iteracionTotal += ReversoNumero(iteracionTotal);
                    if (Palindromo(iteracionTotal.ToString()))
                    {
                        listBox2.Items.Add(i + " Palindromo");
                        break;
                    }
                }
            }
            textBox2.Text = contador.ToString();
        }

Constante de Kaprekar - 6174

El número 6174 es conocido como la Constante de Kaprekar en honor de su descubridor el matemático indio Dattatreya Ramachandra Kaprekar. Este número es el resultado de la aplicación repetida de la Operación de Kaprekar que consiste en los siguientes pasos:

Escoger cualquier número de cuatro dígitos (con limitadas excepciones, véase más abajo).

Ordenar los cuatro dígitos en orden ascendente, para obtener el minuendo de una resta.

Ordenar los mismos cuatro dígitos en orden descendente, para obtener el sustraendo de la misma resta.

Calcular el resto, restando el sustraendo del minuendo.

Si el resto no es igual a 6174, repetir los cuatro pasos anteriores, añadiendo ceros a la derecha al minuendo y a la izquierda al sustraendo, siempre que sea necesario para completar los cuatro dígitos.

Esta operación, repetida si es necesario en varias ocasiones (nunca más de siete veces), termina dando el resultado 6174. El proceso termina porque si se sigue repetiendo la secuencia de pasos, se sigue obteniendo el mismo resultado ya que 7641 – 1467 = 6174.

Por ejemplo, supongamos que partimos del número de cuatro dígitos 5342:

5432 – 2345 = 3087

8730 – 0378 = 8352

8532 – 2358 = 6174


using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace ConstanteKaprekar_I_Forms

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        private void button1_Click(object sender, EventArgs e)

        {

            Application.Exit();

        }

        private void button2_Click(object sender, EventArgs e)

        {

            int numero, res, aux, max2, max3, max4, max, min, ctr, u = 0, d = 0, c = 0, m = 0, max1 = 0;

            string variabletemporal = textBox1.Text;

            if (variabletemporal != null)

            {

                numero = int.Parse(variabletemporal);

                if (numero > 999 && numero <= 9999)

                {

                    do

                    {

                        res = 0;

                        ctr = 0;

                        aux = 0;

                        u = 0;

                        d = 0;

                        c = 0;

                        m = 0;

                        while (numero > 10)

                        {

                            res = numero % 10;

                            switch (aux)

                            {

                                case 0:

                                    {

                                        u = res;

                                        aux++;

                                        break;

                                    }

                                case 1:

                                    {

                                        d = res;

                                        aux++;

                                        break;

                                    }

                                case 2:

                                    {

                                        c = res;

                                        aux++;

                                        break;

                                    }

                            }

                            numero /= 10;

                        }

                        m = numero;

                        max1 = u;

                        max2 = d;

                        max3 = c;

                        max4 = m;

Numeros de Kaprekar

En matemáticas, un número de Kaprekar (Por: Shri Dattatreya Ramachandra Kaprekar, 1905–1986, matemático Indio) es aquel entero no negativo tal que, en una base dada, los dígitos de su cuadrado en esa base pueden ser separados en dos números que sumados dan el número original. El ejemplo más simple es 9, su cuadrado es 81 y 8+1= 9. Otro ejemplo es el número 703, su cuadrado es 494209. Si separamos 494209 en dos nuevos números, 494 y 209, obtenemos que 494 + 209 = 703. De igual forma, el número 297 también es un número de Kaprekar, ya que es posible descomponer el cuadrado 2972 = 88209 en 88 y 209.

El segundo número puede comenzar por cero, pero debe ser positivo. Un ejemplo es 999, ya que 9992=998001 y se descompone en 998 y 001. Por esto mismo, el número 100 no es un número de Kaprekar, ya que 100²=10000 y se descompone en 100 + 00, pero el segundo sumando no es positivo.

Matemáticamente, sea X un entero no negativo. X es un número de Kaprekar para la base b si existen n números enteros no negativos, A y B, que satisfagan las siguientes condiciones:

0 < B < bn

X² = Abn + B

X = A + B


Los primeros números de Kaprekar en base 10 son ((sucesión A006886 en OEIS)):1, 9, 45, 55, 99, 297, 703, ...
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Kaprekar_I_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        ulong numeromaximo;

        private void button2_Click(object sender, EventArgs e)
        {
            numeromaximo = ulong.Parse(textBox1.Text);
            int count = 0;

            foreach (ulong numeromaximo in generador(numeromaximo))
            {
                listBox1.Items.Add(numeromaximo.ToString());
                count++;
                textBox2.Text = count.ToString();
            }
        }

        private static IEnumerable<ulong> generador(ulong max)
        {
            ulong next = 1;

            yield return next;

            for (next = 2; next <= max; next++)
            {
                ulong cuadrado = next * next;

                for (ulong comprobar = 10; comprobar <= 10000000000000000000; comprobar *= 10)
                {

                    if (cuadrado <= comprobar)
                        break;

                    ulong r = cuadrado % comprobar;
                    ulong q = (cuadrado - r) / comprobar;

                    if (r != 0 && q + r == next)
                    {
                        yield return next;
                        break;
                    }
                }

            }
        }
    }
}

Números Amigos - II

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace NumerosAmigos_II_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        int i, numero1, numero2, s1 = 0, s2 = 0;
        string r = "";
        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }
     
        private void button1_Click(object sender, EventArgs e)
        {
            numero1 = int.Parse(textBox1.Text);
            numero2 = int.Parse(textBox2.Text);

            i = 1;
            while (i <= numero1 / 2)
            {
                if (numero1 % i == 0)
                {
                    s1 += i;
                }
                i++;
            }

Números Amigos

Tomemos por ejemplo el número el número 284, que se puede escribir como la multiplicación de los números primos 71 y 2 de la siguiente forma… 284 = 71 x 2 x 2 = 71 x 2 al cuadrado. Así, es fácil de calcular que los divisores del número 284 (sin contar el propio número), son {1, 2, 4, 71, 142}, cuya suma es

1 + 2 + 4 + 71 + 142 = 220.

Si ahora cogemos el número que nos ha salido, 220, y buscamos sus divisores, como 220 = 11 x 5 x 2 x 2, entonces estos son {1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110}, y la suma de estos es
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284,
precisamente el primer número. Por este motivo, se dice que los números 220 y 284 son números amigos. Es decir, dos números son amigos si la suma de los divisores del primero (sin contar al número) es igual al segundo, y viceversa.

Este par de números amigos (220, 284) ya era conocido por los pitagóricos, quienes les atribuían propiedades místicas. En general, en la antigüedad se pensaba que estos números tenían poderes místicos, y eran utilizados en textos religiosos y de magia, en particular, en relación al amor y la amistad. Los astrónomos griegos los incorporaron en sus horóscopos, talismanes y amuletos.

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace NumerosAmigos_Forms_I
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        int numeromaximo;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {

            listBox1.Items.Clear();
            int[] sumas = new int[numeromaximo];

            for (int i = 1; i < sumas.Length; i++)
                sumas[i] = SumaMultiplos(i);

            for (int j = 1; j < sumas.Length; j++)
            {
                int v1 = sumas[j];
                if (v1 > 1 & v1 < sumas.Length)
                {
                    int v2 = sumas[v1];
                    if (v2 == j && v1 > v2)
                        listBox1.Items.Add(v2.ToString() + "  <-->  " + v1.ToString());
                }
            }
        }

Números Catalan

En combinatoria, los números de Catalan forman una secuencia de números naturales que aparece en varios problemas de conteo que habitualmente son recursivos. Obtienen su nombre del matemático belga Eugène Charles Catalan (1814–1894).

El n-ésimo número de Catalan se obtiene, aplicando coeficientes binomiales, a partir de la siguiente fórmula:

Los números de Catalan satisfacen la siguiente relación de recurrencia:

Y también satisfacen:

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

namespace NumerosCatalan_Forms_II

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        int numero;

        private void button1_Click(object sender, EventArgs e)

        {

            Application.Exit();

        }

        private void button2_Click(object sender, EventArgs e)

        {

            GeneradorNumerosCatalanes generator = new GeneradorNumerosCatalanes();

            for (int i = 0; i <= numero; i++)

            {

                textBox1.Text += "Numero Catalan 1ª Opción: " + " " + (i.ToString() + "-> " + (generator.PrimeraOpcion((i)) + "\r\n"));

                textBox1.Text += "Numero Catalan 2ª Opción: " + " " + (i.ToString() + "-> " + (generator.SegundaOpcion((i)) + "\r\n"));

                textBox1.Text += "Numero Catalan 3ª Opción: " + " " + (i.ToString() + "-> " + (generator.TerceraOpcionn((i)) + "\r\n"));

            }

        }

Conjetura de los Números Primos Gemelos

Dos números primos se denominan gemelos si uno de ellos es igual al otro más dos unidades. Así pues, los números primos 3 y 5 forman una pareja de primos gemelos. Otros ejemplos de pares de primos gemelos son 11 y 13 ó 41 y 43.

La conjetura de los primos gemelos postula la existencia de infinitos pares de primos gemelos. Dado que es una conjetura, está todavía sin demostrar.

Existe un número infinito de primos p tales que p + 2 también es primo.

La conjetura ha sido investigada por muchos teóricos de números. La mayoría de matemáticos cree que la conjetura es cierta, y se basan en evidencias numéricas y razonamientos heurísticos sobre la distribución probabilística de los números primos.

En 1849, Alphonse de Polignac formuló una conjetura más general según la cual, para todo número natural k existen infinitos pares de primos cuya diferencia es 2·k. El caso k=1 es la conjetura de los números primos gemelos.

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

namespace PrimosGemelos_Forms

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        private void button2_Click(object sender, EventArgs e)

        {

            Application.Exit();

        }

        private void button1_Click(object sender, EventArgs e)

        {

            int n;

            int p, q, encontrados;

            int contar;

            p = 1;

            encontrados = 0;

            contar = 1;

            n = int.Parse(textBox2.Text);

            while (encontrados < n)

            {

                q = p + 2;

                if (es_primo(p) != 1 && es_primo(q) != 1)

                {

                    listBox1.Items.Add(p.ToString() + " - " + q.ToString() + " -> Son Primos Gemelos.   -  " + contar++.ToString());

                    encontrados++;

                }

                p++;

            }

        }

Cuadrado Magico

Un cuadrado mágico es una tabla de grado primario donde se dispone de una serie de números enteros en un cuadrado o matriz de forma tal que la suma de los números por columnas, filas y diagonales principales sea la misma. Usualmente los números empleados para rellenar las casillas son consecutivos, de 1 a n², siendo n el número de columnas y filas del cuadrado mágico. Los cuadrados mágicos actualmente no tienen ninguna aplicación técnica conocida que se beneficien de estas características, por lo que sigue recluido al divertimento, curiosidad y al pensamiento matemático. Aparte de esto, en las llamadas seudo ciencias ocultas y más concretamente en la magia tienen un lugar destacado.

Fachada de la Sagrada Familia

La Fachada de la Pasión del Templo Expiatorio de la Sagrada Familia en Barcelona, diseñada por el escultor Josep María Subirachs, muestra un cuadrado mágico de orden 4.

La constante mágica del cuadrado es 33, la edad de Jesucristo en la Pasión. También se ha atribuido la elección de este número como una velada alusión a la supuesta adscripción masónica, que nunca ha sido demostrada, de Antonio Gaudí, ya que 33 son los grados tradicionales de la masonería. Estructuralmente, es muy similar al cuadrado mágico de Melancolía, pero dos de los números del cuadrado (el 12 y el 16) están disminuidos en dos unidades (10 y 14) con lo que aparecen repeticiones. Esto permite rebajar la constante mágica en 1.

Consideremos la sucesión matemática 1, 2, 3, 4... 36 (cuadrado de orden 6), y dispongamos los números ordenadamente en dos series dispuestas en zig-zag:

1   2   3   4   5   6   7   8   9 10 11 12 13 14 15 16 17 18
36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19

Resulta evidente que cualquier par de números alineados verticalmente suma lo mismo ya que a medida que nos desplazamos por las columnas, en la fila superior se añade una unidad, mientras que en la fila inferior se resta. La suma es en todos los casos la de los números extremos:

Si disponemos el conjunto de números en seis filas (ver tabla a la derecha), fácilmente se puede apreciar que las sumas en las distintas columnas han de ser necesariamente iguales, ya que los números se encuentran agrupados por pares tal y como estaban en el primer caso (compárese los pares de filas 1ª-6ª, 2ª-5ª y 3ª-4ª con la disposición original). Ahora sin embargo, por ser tres los pares de filas (n/2), la suma será:

${\displaystyle M_{2}(n)={\frac {n(n^{2}+1)}{2}}}$

cantidad que se denomina constante mágica, y que en nuestro caso es n×(n² + 1)/2 = 6×(36 + 1)/2 = 111.

Orden n	3	4	5	6	7	8	9	10	11	12	13
M2 (n)	15	34	65	111	175	260	369	505	671	870	1105

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace CuadradoMagico_I_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            int n;
            n = int.Parse(textBox2.Text);

Función de Ackermann

Wilhelm Ackermann (29 de marzo 1896 - 24 de diciembre 1962) fue un matemático alemán. Es conocido, sobre todo, por la función de Ackermann nombrada en su honor, un ejemplo importante en la teoría de la computación.

En teoría de la computación, función de Ackermann es una función matemática recursiva encontrada en 1926 por Wilhelm Ackermann, tiene un crecimiento extremadamente rápido, de interés para la ciencia computacional teórica y la teoría de la computabilidad. Hoy en día, hay una serie de funciones que son llamadas funciones Ackermann. Todas ellas tienen una forma similar a la ley original la función de Ackermann y también tienen un comportamiento de crecimiento similar. Esta función toma dos números naturales como argumentos y devuelve un único número natural. Como norma general se define como sigue:

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Ackerman_IV
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            for (long m = 0; m <= 3; ++m)
            {
                for (long n = 0; n <= 4; ++n)
                {
                    textBox1.AppendText(string.Format("Ackerman({0},{1}) = {2}", m, n, Ackermann(m, n))+"\r\n");            
                }
            }

Números Palíndromos

Un palíndromo (del griego palin dromein, volver a ir atrás), también llamado palindromo, palíndroma o palindroma, es una palabra, número o frase que se lee igual adelante que atrás. Si se trata de un numeral, usualmente en notación indoarábiga, se llama capicúa.

La palabra capicúa (del catalán cap i cua, «cabeza y cola») (en matemáticas, número palíndromo) se refiere a cualquier número que se lee igual de izquierda a derecha que derecha a izquierda. Ejemplos: 161, 2992, 3003, 2882

Un número palindrómico es un número de n dígitos escrito en cualquier base b (bn-1bn-2...b1b0) tal que bi = bn-1-i.

Todos los números de base 10 con un dígito {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} son palindrómicos.

Es una sucesión finita, tal que el primero y el último, el segundo y el penúltimo términos... y así sucesivamente son iguales. O bien el término de orden i tiene el mismo valor que el de orden n-i.

Ejemplo: (14641) 1, 4, 6, 4, 1.

Se observa que los extremos 1 y 1 están a igual distancia del elemento central "6"; la diferencia entre ellos es cero. Los intermedios 4 y 4 asumen la misma propiedad que los anteriores. Y el 6 dista cero unidades lineales de sí mismo y su diferencia es cero. Esto es, pues, lo que se denomina la simetría capicual.

Si la suma de una progresión geométrica, con primer término 1 y razón x, se eleva a una potencia entera positiva los respectivos coeficientes se disponen en sucesión capicual.

Todo capicúa con un número par de cifras es divisible por 11.

Se obtiene el capicúa de un número sumando el número con su reverso, hasta obtener su capicúa. Ej: calcular el capicúa del número 57 57+75=132, 132+231=363

El capicúa del número 57 es 363. Todos los números tienen su capicúa.

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

namespace Palindromo_III

    {

    public partial class Form1 : Form

        {

        public Form1()

            {

            InitializeComponent();

            }

        // Variables

        int numero1, numero2;

        private void button2_Click(object sender, EventArgs e)

            {

            numero1 = int.Parse(textBox1.Text);

            numero2 = int.Parse(textBox2.Text);

            intervalo(numero1, numero2);

            }

Triangulo de Pascal

El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos.

El Triángulo de Pascal o Tartaglia tiene un origen, como en muchos otros casos, muy anterior al de estos dos matemáticos . Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el poeta persa Omar Khayyam (siglo XII).

El que se le asocie el nombre del filósofo, matemático Pascal (1623-1662) se debe a que el francés escribió el primer tratado sobre el triángulo. Lo de Tartaglia (1500-1557) viene porque el italiano fue de los primeros que lo publicaron en Europa.

Cada número es la suma de los dos números que tiene encima, menos los extremos, que son siempre "1".

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace TrianguloPascal_III
    {
    public partial class Form1 : Form
        {
        public Form1()
            {
            InitializeComponent();
            }

        private void button2_Click(object sender, EventArgs e)
            {
            Application.Exit();
            }
        //Variables
       int numero;

        private void button1_Click(object sender, EventArgs e)
            {
            for (int y = 0; y < numero; y++)
                {
                int c = 1;
                for (int q = 0; q < numero - y; q++)
                    {
                    textBox2.Text += "   ";
                    }
                    for (int x = 0; x <= y; x++)
                        {
                        textBox2.AppendText(c.ToString());
                        textBox2.Text += "    " + "\n";
                        c = c * (y - x) / (x + 1);
                        }
                    textBox2.Text += "   \r\n";
                    }
                }
       

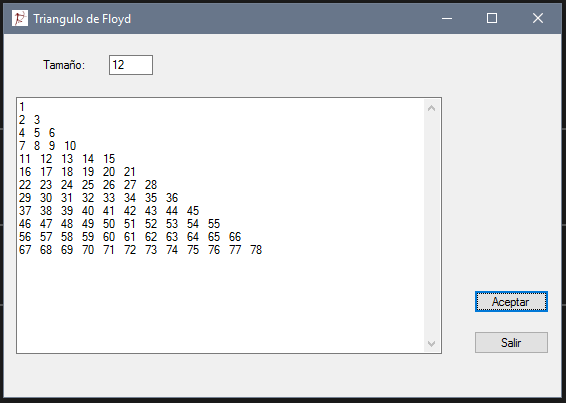
Triangulo de Floyd

El Triángulo de Floyd, llamado así en honor a Robert Floyd, es un triángulo rectángulo formado con números naturales. Para crear un triángulo de Floyd, se comienza con un 1 en la esquina superior izquierda y se continúa escribiendo la secuencia de los números naturales de manera que cada línea contenga un número más que la anterior:

1
2 3
4 5 6
7 8 9 10
11 12 13 14 15

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Floyd_I
    {
    public partial class Form1 : Form
        {
        public Form1()
            {
            InitializeComponent();
            }
        //Variables
        int i, j, k = 1, tamano;
        

        private void textBox2_TextChanged(object sender, EventArgs e)
            {
            tamano = Convert.ToInt32(textBox2.Text);
            }

        private void button3_Click(object sender, EventArgs e)
            {
            Application.Exit();
            }
 

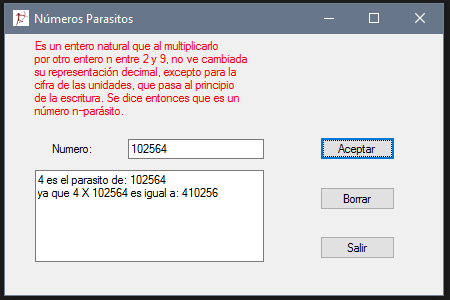
Números Parasitos

Resultan ser curiosos números que al ser multiplicados por su última cifra queda exactamente el mismo número pero con esa misma última cifra corrida hacia la izquierda; por ejemplo, tenemos que:
102.564 x 4=410.256 ¿Curioso verdad!? lo mejor es que existe una fórmula para encontrar p-parásitos
p/(10p-1) de forma que nos saldrá un número decimal; con ese número decimal omitimos la coma y truncamos en el momento en que haya un dígito que tome el valor de p (a veces no es el primero). Siguiendo el ejemplo anterior, resultaría que queremos encontrar un 4-parásito. Sustituimos en la fórmula y nos queda 4/39=0,10256410..., omitimos la coma y trunco hasta un dígito que tome el valor 4, así que nos queda, efectivamente, 102.564, que como puse más arriba es un ejemplo de número parásito(4-parásito), se puede hacer para más valores de p, pero, repito, no siempre vale con truncar hasta el primer dígito que tome el valor p, a veces hay que llegar más allá, pero el caso es que con la curiosa fórmula p/(10p-1) encontramos números parásitos.

Si no coincide el dígito de las unidades con el dígito multiplicador, se dice que el número es un pseudoparásito. Por ejemplo, 179487 es un 4-pseudoparásito, porque 179487 x 4 = 717948.


using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace N_Parasito_II
    {
    public partial class Form1 : Form
        {
        public Form1()
            {
            InitializeComponent();
            }

        private void button3_Click(object sender, EventArgs e)
            {
            Application.Exit();
            }

        private void button2_Click(object sender, EventArgs e)
            {
            textBox1.Clear();
            textBox2.Clear();
            }

        private void button1_Click(object sender, EventArgs e)
            {
            int numero = int.Parse(textBox1.Text);
            int temporal = numero, contador = 0;
            List<int> c = new List<int>();

Números Armstrong

Un número es ARMSTRONG si la suma de los dígitos elevados a la cantidad de dígitos que lo componen es igual al número.

Parece ser que son llamados números Armstrong, debido al nombre de un profesor de matemáticas de la Universidad de Rochester, que durante una clase puso un ejercicio de este tipo a sus alumnos, no obstante ya habían sido identificados por algunos matemáticos (Godfrey H. Hardy), pero Armstrong fue el primero en explorar este concepto.

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Armstrong_IX
    {
    public partial class Form1 : Form
        {
        public Form1()
            {
            InitializeComponent();
            }

        private void button2_Click(object sender, EventArgs e)
            {
            Application.Exit();
            }

        private void button1_Click(object sender, EventArgs e)
            {
            Armstrong n = new Armstrong();
            int c = 0, x = 0, numero;
            numero = Convert.ToInt32(textBox1.Text);           
            while (c < numero)
                {
                if (n.isArmstrong(x))
                    {                   
                     textBox2.AppendText ( Convert.ToString(x)+"\n");                   
                 c++;
                    }
                 x++;
                }
            }