Figura - XVIII

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XIX_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        int n = 1;
        char r, c, ch;

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            ch = Convert.ToChar(textBox2.Text);
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

Figura - XVII

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XVIII_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        char ch, r, c, p, z;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            ch = Convert.ToChar(textBox2.Text);
        }

        private void button1_Click(object sender, EventArgs e)
        {
            if (ch >= 'a' && ch <= 'z')
            {
                ch = (char)(ch - 32);
            }
            textBox1.Text += "\r\n";

            for (r = 'A', z = ch; r <= ch; r++, z--)
            {
                for (c = r, p = z; c >= 'A'; c--, p++)
                {
                    textBox1.Text += (p.ToString());
                }
                for (c = r, p = (char)(ch - 1); c > 'A'; c--, p--)
                {
                    textBox1.Text += (p.ToString());
                }
                textBox1.Text += "\r\n";
            }

Figura - XVI

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XVII_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        char ch, r, c;

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            ch = Convert.ToChar(textBox2.Text);
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

Figura - XV

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XVI_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        char r, c, ch, h;

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            ch = Convert.ToChar(textBox2.Text);
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

Figura - XIV

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XV_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        int num;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1; r <= num; r++)
            {
                for (int sp = num - r; sp >= 1; sp--)
                {
                    textBox1.Text += " ";
                }
                textBox1.Text += (r.ToString());
                for (int sp = r * 2; sp > 1; sp--)
                {
                    textBox1.Text += " ";
                }
                textBox1.Text += (r.ToString());
                textBox1.Text += "\r\n";

Figura - XIII

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XIV_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }
        int num, z = 1, p, n;
        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1; r <= num; r++, z = z + 2)
            {
                for (int c = 1; c <= z; c++)
                {
                    if (c % 2 == 0)
                    {
                        textBox1.Text += "*";
                    }
                    else
                    {
                        textBox1.Text += (r.ToString());
                    }
                }
                textBox1.Text += "\r\n";
            }

Figura - XII

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XIII_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            textBox1.Text += "1" + "\r\n";
            for (int r = 2; r <= 20; r++)
            {
                for (int c = 1; c <= r; c++)
                {
                    if (c == r)
                    {
                        textBox1.Text += (r.ToString());
                    }

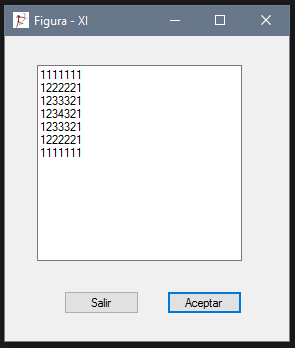
Figura - XI

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XII_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        int num = 4, q = 6;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
         
            for (int r = 1; r <= num; r++, q = q - 2)
            {
                for (int c = 1; c <= r; c++)
                {
                    textBox1.Text += (c.ToString());
                }
                for (int p = q; p >= 1; p--)
                {
                    textBox1.Text += (r.ToString());
                }
                for (int c = r - 1; c >= 1; c--)
                {
                    textBox1.Text += (c.ToString());
                }
                textBox1.Text += "\r\n";

Figura - X

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_XI_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }
        int num, y;

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            num = int.Parse(textBox2.Text);
        }

        private void button1_Click(object sender, EventArgs e)
        {
            y = num + 1;

            for (int r = 1; r <= num; r++, y--)
            {
                for (int c = 1, n = num; c <= r; c++, n--)
                {
                    textBox1.Text += ("  " + n.ToString());
                }
                for (int c = 1, p = y; c < r; c++, p++)
                {
                    textBox1.Text += ("  " + p.ToString());
                }
                textBox1.Text += "\r\n";

Figura - IX

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_X_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        int num, n;
        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void textBox2_TextChanged(object sender, EventArgs e)
        {
            num = int.Parse(textBox2.Text);
        }

        private void button1_Click(object sender, EventArgs e)
        {
            n = num;
            for (int r = 1; r <= num; r++, n--)
            {
                for (int c = n; c <= num; c++)
                {
                    textBox1.Text += (c.ToString());
                }
                for (int c = r, j = num + 1; c > 1; c--, j++)
                {
                    textBox1.Text += (j.ToString());
                }
                textBox1.Text += "\r\n";
            }

Figura - VIII

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_IX_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1, n = 1; r <= 12; r++, n = n + 2)
            {
                if (r % 2 == 0)
                {
                    for (int c = 1, p = 2; c <= n; c++, p = p + 2)
                    {
                        textBox1.Text += ("  " + p.ToString());
                    }
                }

Figura - VII

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_VIII_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            int n = 4, p = 4, x = 1;
            for (int r = 1; r <= n; r++)
            {
                for (int c = 1; c <= r; c++, x++)
                {
                    textBox1.Text += (" " + x.ToString());
                }
                textBox1.Text += "\r\n";
            }

Figura - VI

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_VII_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        int num, q;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1, n = num; r <= num; r++, n--)
            {
                for (int c = r, p = n; c >= 1; c--, p++)
                {
                    textBox1.Text += (p.ToString());
                }
                for (int c = r, p = num - 1; c > 1; c--, p--)
                {
                    textBox1.Text += (p.ToString());
                }
                textBox1.Text += "\r\n";
            }

Figura - V

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_VI_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        int num, n;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            n = num;
            for (int r = 1; r <= num; r++, n--)
            {
                for (int c = 1; c <= n; c++)
                {
                    textBox1.Text += (c.ToString());
                }

Figura - IV

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_V_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        int num;
        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1, m = 0; r <= num + 1; r++, m++)
            {
               
                for (int c = 1, n = m; c <= r; c++, n--)
                {
                    textBox1.Text += (n.ToString());
                }

Figura - III

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_IV_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }
        int num;

        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1, n = num; r <= num; r++, n--)
            {
                for (int sp = r; sp > 1; sp--)
                {

                    textBox1.Text += "  ";
                }
                for (int c = r, p = n; c <= num; c++, p--)
                {
                    textBox1.Text += (p.ToString());

Figura - II

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_III_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        int num;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

Figura - I

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Triangulo_II_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }
        int num;

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            for (int r = 1; r <= num; r++)
            {
                for (int sp = num - r; sp > 0; sp--)
                {
                    textBox1.Text += "   ";

                }
                for (int c = 1; c <= r; c++)
                {
                    textBox1.Text += (r.ToString());
                    textBox1.Text += " ";
                    //textBox1.Text += (" " + (c.ToString()));
     

ZX-81 Emulador EightyOne

La computadora Sinclair ZX81 era pequeña, negra y contaba con sólo 1 KB de memoria, pero hace 36 años ayudó a crear una generación de grandes programadores.

El computador personal Sinclair ZX81, lanzado por Sinclair Research en 1981, fue el computador de menor precio de la época. Este era la versión mejorada del ZX80 comercializado el año anterior. La carcasa era negra, con un teclado de membrana. La apariencia definitiva de la máquina fue el trabajo del diseñador industrial Rick Dickinson. La salida de vídeo, como en el ZX80, era hacia un televisor por medio de un modulador de radiofrecuencia, y los programas se leían y se guardaban a través de un ordinario grabador de casetes usando cintas magnéticas de audio.

Es un ordenador muy simple, con tan solo cuatro chips:
CPU: CPU NEC D780 C (clon del Z80 o Z80 A, a 3.25 MHz.
ROM: 8 Kb.
RAM: 1 Kb ampliable hasta 64 Kb (16 Kb es lo usual).
ULA: reemplazaba a los 18 Circuitos Integrados que se utilizaban en el anterior modelo ZX80, lo que produjo una reducción tanto en espacio como en costes de producción y venta.

El ZX81 es el primer triunfo de Sir Clive Sinclair y representa la punta de lanza de la penetración del ordenador en el hogar. La reducida memoria del ZX81 tiene dos consecuencias:
Populariza la ampliacion de 16 Kb como el primer periférico a adquirir.
Incentiva la creatividad de los programadores (se escribieron hasta juegos de ajedrez para 1Kb), implantando el ahorro de memoria y la optimización de los programas.Fue mi primer ordenador el cual todavía conservo. El problema que tenia era el sistema de almacenamiento, por lo demás fueron mis primeros pasos en un lenguaje de programación. Es una lastima que perdí el manual que traía y no lo he conseguido.

Este emulador es una maravilla, te permite elegir entre toda la gama de productos Sinclair de la época, con todas las configuraciones de memoria y periféricos que quieras añadir, la verdad es que me trae muy buenos recuerdos.
No requiere instalación, simplemente descomprimirlo en un directorio.

Enlace de descarga del emulador:

https://www.aptanet.org/eightyone/

https://sourceforge.net/projects/eightyone-sinclair-emulator/

https://es.wikipedia.org/wiki/Sinclair_ZX81

Cuadrado Magico

Un cuadrado mágico es una tabla de grado primario donde se dispone de una serie de números enteros en un cuadrado o matriz de forma tal que la suma de los números por columnas, filas y diagonales principales sea la misma. Usualmente los números empleados para rellenar las casillas son consecutivos, de 1 a n², siendo n el número de columnas y filas del cuadrado mágico. Los cuadrados mágicos actualmente no tienen ninguna aplicación técnica conocida que se beneficien de estas características, por lo que sigue recluido al divertimento, curiosidad y al pensamiento matemático. Aparte de esto, en las llamadas seudo ciencias ocultas y más concretamente en la magia tienen un lugar destacado.

Fachada de la Sagrada Familia

La Fachada de la Pasión del Templo Expiatorio de la Sagrada Familia en Barcelona, diseñada por el escultor Josep María Subirachs, muestra un cuadrado mágico de orden 4.

La constante mágica del cuadrado es 33, la edad de Jesucristo en la Pasión. También se ha atribuido la elección de este número como una velada alusión a la supuesta adscripción masónica, que nunca ha sido demostrada, de Antonio Gaudí, ya que 33 son los grados tradicionales de la masonería. Estructuralmente, es muy similar al cuadrado mágico de Melancolía, pero dos de los números del cuadrado (el 12 y el 16) están disminuidos en dos unidades (10 y 14) con lo que aparecen repeticiones. Esto permite rebajar la constante mágica en 1.

Consideremos la sucesión matemática 1, 2, 3, 4... 36 (cuadrado de orden 6), y dispongamos los números ordenadamente en dos series dispuestas en zig-zag:

1   2   3   4   5   6   7   8   9 10 11 12 13 14 15 16 17 18
36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19

Resulta evidente que cualquier par de números alineados verticalmente suma lo mismo ya que a medida que nos desplazamos por las columnas, en la fila superior se añade una unidad, mientras que en la fila inferior se resta. La suma es en todos los casos la de los números extremos:

Si disponemos el conjunto de números en seis filas (ver tabla a la derecha), fácilmente se puede apreciar que las sumas en las distintas columnas han de ser necesariamente iguales, ya que los números se encuentran agrupados por pares tal y como estaban en el primer caso (compárese los pares de filas 1ª-6ª, 2ª-5ª y 3ª-4ª con la disposición original). Ahora sin embargo, por ser tres los pares de filas (n/2), la suma será:

${\displaystyle M_{2}(n)={\frac {n(n^{2}+1)}{2}}}$

cantidad que se denomina constante mágica, y que en nuestro caso es n×(n² + 1)/2 = 6×(36 + 1)/2 = 111.

Orden n	3	4	5	6	7	8	9	10	11	12	13
M2 (n)	15	34	65	111	175	260	369	505	671	870	1105

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace CuadradoMagico_I_Forms
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            int n;
            n = int.Parse(textBox2.Text);

Validar IBAN - International Bank Account Number

El International Bank Account Number (IBAN) Código Internacional de Cuenta Bancaria, en español es un código alfanumérico que identifica una cuenta bancaria determinada en una entidad financiera en cualquier lugar del mundo (si el país está adherido al sistema IBAN). Es decir, a cada cuenta le corresponde un único IBAN mediante el cual se identifica el país, la entidad, la oficina y la cuenta. Se trata de un estándar (EBS204) del Comité Europeo de Estándares Bancarios, que a su vez cumple con el estándar ISO 13616. En España, el código IBAN sustituyó de manera definitiva al Código Cuenta Cliente (CCC) el 1 de febrero de 2014.

El objetivo del IBAN es facilitar el tratamiento automático de pagos y cobros transfronterizos. El estándar asegura la transmisión correcta de los datos y reduce las posibilidades de intervención manual. Por tanto contribuye a evitar los costes y las demoras asociadas a la transmisión incorrecta o insuficiente de los datos relativos a las cuentas bancarias.

using System;

using System.Collections.Generic;

using System.ComponentModel;

using System.Data;

using System.Drawing;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

using System.Windows.Forms;

namespace IBAN_V

{

    public partial class Form1 : Form

    {

        public Form1()

        {

            InitializeComponent();

        }

        string iban;

        

         

private void button2_Click(object sender, EventArgs e)

        {

            Application.Exit();

        }

       

          

        private void button1_Click(object sender, EventArgs e)

        {

            if (validarIBAN(iban) == true)

            {

                MessageBox.Show("IBAN Correcto");

            }

            else

            {

                MessageBox.Show("Algo funciona mal");

            }

        }

            bool validarIBAN(string iban)

            {

                iban = textBox1.Text;

                if (iban.Length < 4 || iban[0] == ' ' || iban[1] == ' ' || iban[2] == ' ' || iban[3] == ' ') throw new InvalidOperationException();

                var checksum = 0;

                var ibanLength = iban.Length;

                for (int charIndex = 0; charIndex < ibanLength; charIndex++)

                {

                    if (iban[charIndex] == ' ') continue;

Función de Ackermann

Wilhelm Ackermann (29 de marzo 1896 - 24 de diciembre 1962) fue un matemático alemán. Es conocido, sobre todo, por la función de Ackermann nombrada en su honor, un ejemplo importante en la teoría de la computación.

En teoría de la computación, función de Ackermann es una función matemática recursiva encontrada en 1926 por Wilhelm Ackermann, tiene un crecimiento extremadamente rápido, de interés para la ciencia computacional teórica y la teoría de la computabilidad. Hoy en día, hay una serie de funciones que son llamadas funciones Ackermann. Todas ellas tienen una forma similar a la ley original la función de Ackermann y también tienen un comportamiento de crecimiento similar. Esta función toma dos números naturales como argumentos y devuelve un único número natural. Como norma general se define como sigue:

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace Ackerman_IV
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void button2_Click(object sender, EventArgs e)
        {
            Application.Exit();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            for (long m = 0; m <= 3; ++m)
            {
                for (long n = 0; n <= 4; ++n)
                {
                    textBox1.AppendText(string.Format("Ackerman({0},{1}) = {2}", m, n, Ackermann(m, n))+"\r\n");            
                }
            }